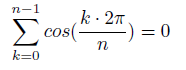-
Liebe User, bitte beachtet folgendes Thema: Was im Forum passiert, bleibt im Forum! Danke!
Mathe Rätsel Marathon
- Ersteller Brusko651
- Erstellt am
- Mitglied seit
- 22.03.2008
- Beiträge
- 1.672
- Reaktionen
- 0
ich geb mal 1-2 Tipps:
Tipp1:
Es ist sinnvoll, je zwei Brüche, die die selben zwei Variablen enthalten, auf einen Nenner zu bringen, und zusammenzufassen.
Tipp2:
Jemand legt drei Stapel mit Geldscheinen auf Dagobert Ducks Schreibtisch, und sagt ihm, er darf sich von einem der Stapel 20 Geldscheine nehmen, von einem anderen 7 Scheine und vom letzten 2 Scheine.
Einer der Stapel besteht aus 100$ Noten, einer aus 50$ Noten und einer aus 5$ Noten.
Was macht Dagobert Duck?
Er nimmt sich natürlich 20 Scheine vom 100-er Stapel, 7 vom 50-er Stapel und 2 vom 5-er Stapel. Dadurch erhält er 20*100 + 7 * 50 + 2*5 $, und mehr hätte er nicht bekommen können.
Das ist das Grundprinzip der Ordnungsungleichung.
http://de.wikipedia.org/wiki/Umordnungs-Ungleichung
Man braucht die Ordnungsungleichung übrigens nicht zwangsläufig, um die Ungl. zu beweisen, aber sie macht's einfacher.
Tipp1:
Es ist sinnvoll, je zwei Brüche, die die selben zwei Variablen enthalten, auf einen Nenner zu bringen, und zusammenzufassen.
Tipp2:
Jemand legt drei Stapel mit Geldscheinen auf Dagobert Ducks Schreibtisch, und sagt ihm, er darf sich von einem der Stapel 20 Geldscheine nehmen, von einem anderen 7 Scheine und vom letzten 2 Scheine.
Einer der Stapel besteht aus 100$ Noten, einer aus 50$ Noten und einer aus 5$ Noten.
Was macht Dagobert Duck?
Er nimmt sich natürlich 20 Scheine vom 100-er Stapel, 7 vom 50-er Stapel und 2 vom 5-er Stapel. Dadurch erhält er 20*100 + 7 * 50 + 2*5 $, und mehr hätte er nicht bekommen können.
Das ist das Grundprinzip der Ordnungsungleichung.
http://de.wikipedia.org/wiki/Umordnungs-Ungleichung
Man braucht die Ordnungsungleichung übrigens nicht zwangsläufig, um die Ungl. zu beweisen, aber sie macht's einfacher.
Zuletzt bearbeitet:
Solche Bruchumformungen sind doch doof 
.
Bringe die rechte Seite auf die linke Seite, sodass die Ungleichung zu
(1-a)/(1-b) - (1+a)/(1+b) +- ... >=? 0
wird.
Fasse die Terme nun paarweise zusammen und vereinfache den Zähler:
(2b-2a)/(1-b^2) + (2c-2b)/(1-c^2) + (2a-2c)/(1-c^2)
Ignoriere den konstanten Faktor von 2 (wir schätzen später gegen 0 ab und 0/2=0).
Definiere f(x)=1/(1-x^2), diese Funktion ist monoton steigend im Bereich (0,1).
Der Term lässt sich damit neu zusammenfassen und schreiben als
b(f(b)-f(c)) + c(f(c)-f(a)) + a(f(a)-f(b))
Sei nun oBdA a>=b>=c (Fall 1) oder a<=b<=c (Fall 2) - der Term ist zwar invariant gegenüber einer Rotation der Variablen, aber die Vertauschung zweier Variablen gibt einen anderen Term.
Definiere außerdem x=a-c (und damit a=c+x) und y=b-c (und damit b=c+y).
Eingesetzt in die Faktoren vor den jeweiligen Klammern vereinfacht sich der Term damit zu
x(f(a)-f(c)) + y(f(b)-f(c))
In Fall 1 ist x,y>=0 und beide Klammern sind positiv, also ist der Ausdruck >=0
In Fall 2 sind x,y<=0 und beide Klammern sind negativ, also ist der Ausdruck >=0
Fertig.
Rätsel #25
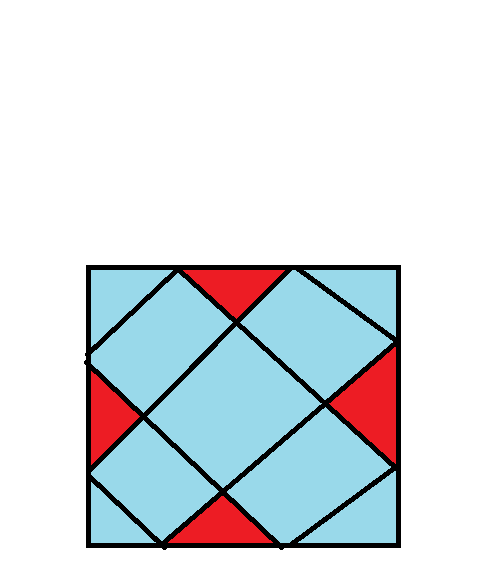
Die Standard-Möglichkeit, einen Würfel aus Papier zu basteln, ist ein Würfelnetz wie dieses auszuschneiden und zusammenzuklappen.
Selbst wenn man ein rechteckiges Papier im idealen Format hat (hier: 4:3), geht ein großer Teil des Papiers verloren - 50% im Beispiel. Wie kann man das Muster verbessern, um (mit geeignetem Papierformat) 3/4 der Fläche zu nutzen? Dabei dürfen auch Würfelseiten "zerlegt" werden, solange sich das Objekt danach ohne Kleber etc. zu einem vollständigen Würfel mit 6 vollständigen Seiten zusammenfalten lässt.
.Bringe die rechte Seite auf die linke Seite, sodass die Ungleichung zu
(1-a)/(1-b) - (1+a)/(1+b) +- ... >=? 0
wird.
Fasse die Terme nun paarweise zusammen und vereinfache den Zähler:
(2b-2a)/(1-b^2) + (2c-2b)/(1-c^2) + (2a-2c)/(1-c^2)
Ignoriere den konstanten Faktor von 2 (wir schätzen später gegen 0 ab und 0/2=0).
Definiere f(x)=1/(1-x^2), diese Funktion ist monoton steigend im Bereich (0,1).
Der Term lässt sich damit neu zusammenfassen und schreiben als
b(f(b)-f(c)) + c(f(c)-f(a)) + a(f(a)-f(b))
Sei nun oBdA a>=b>=c (Fall 1) oder a<=b<=c (Fall 2) - der Term ist zwar invariant gegenüber einer Rotation der Variablen, aber die Vertauschung zweier Variablen gibt einen anderen Term.
Definiere außerdem x=a-c (und damit a=c+x) und y=b-c (und damit b=c+y).
Eingesetzt in die Faktoren vor den jeweiligen Klammern vereinfacht sich der Term damit zu
x(f(a)-f(c)) + y(f(b)-f(c))
In Fall 1 ist x,y>=0 und beide Klammern sind positiv, also ist der Ausdruck >=0
In Fall 2 sind x,y<=0 und beide Klammern sind negativ, also ist der Ausdruck >=0
Fertig.
Rätsel #25
Die Standard-Möglichkeit, einen Würfel aus Papier zu basteln, ist ein Würfelnetz wie dieses auszuschneiden und zusammenzuklappen.
Selbst wenn man ein rechteckiges Papier im idealen Format hat (hier: 4:3), geht ein großer Teil des Papiers verloren - 50% im Beispiel. Wie kann man das Muster verbessern, um (mit geeignetem Papierformat) 3/4 der Fläche zu nutzen? Dabei dürfen auch Würfelseiten "zerlegt" werden, solange sich das Objekt danach ohne Kleber etc. zu einem vollständigen Würfel mit 6 vollständigen Seiten zusammenfalten lässt.
Zuletzt bearbeitet:
- Mitglied seit
- 22.03.2008
- Beiträge
- 1.672
- Reaktionen
- 0
endlich löst das mal jemand. 
Und sogar ohne die Ordnungsungleichung.
Das mit der Ordnungsungl. wäre so gegangen:
Weil die Funtkion f (wie in mfb's post definiert) monoton steigend ist, sind a,b,c und f(a),f(b),f(c) gleich geordnet (also zB b>=a>=c => f(b)>=f(a)>=f(c)), und somit nach der Ordnungs-Ungleichung:
a*f(a) + b*f(b) + c*f(c) >= b*f(a) + c*f(b) + a*f(c),
was zu zeigen war.
Und sogar ohne die Ordnungsungleichung.
Das mit der Ordnungsungl. wäre so gegangen:
Weil die Funtkion f (wie in mfb's post definiert) monoton steigend ist, sind a,b,c und f(a),f(b),f(c) gleich geordnet (also zB b>=a>=c => f(b)>=f(a)>=f(c)), und somit nach der Ordnungs-Ungleichung:
a*f(a) + b*f(b) + c*f(c) >= b*f(a) + c*f(b) + a*f(c),
was zu zeigen war.
- Mitglied seit
- 22.03.2008
- Beiträge
- 1.672
- Reaktionen
- 0
Ich poste nochmal ein neues:
(es ist kein Doppelpost, wenn dazwischen ein Tag vergangen ist ;-). Aber nachdem es jetzt schon ein triple post ist, könnte ja ein mod die vorherigen beiden posts zusammenlegen. ich mach nur doppelpost, damit man sieht, dass ein neuer post da ist.)
rätsel #26:
Finde den Rest von
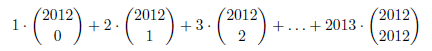
bei Division durch 2012.
(es ist kein Doppelpost, wenn dazwischen ein Tag vergangen ist ;-). Aber nachdem es jetzt schon ein triple post ist, könnte ja ein mod die vorherigen beiden posts zusammenlegen. ich mach nur doppelpost, damit man sieht, dass ein neuer post da ist.)
rätsel #26:
Finde den Rest von
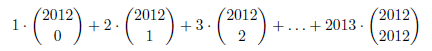
bei Division durch 2012.
@Bild: Ja, das ist auch die beste Lösung die ich kenne.
@Rest:
Zerlege die Summe zunächst in
(2012 über 0) + (2012 über 1) + ... + (2012 über 2012)
+ 0*(2012 über 0) + 1*... + 2012*(2012 über 2012)
Der erste Teil gibt genau 2^2012, was äquivalent zu 16 (mod 2012) ist. Kann man nachrechnen, auch wenn es auf dem Papier etwas Aufwand bedeutet.
Da (2012 über k) = (2012 über 2012-k), kann man die Summanden des zweiten Teils jeweils von außen paarweise zusammenfassen zu
2012*(2012 über 0) + 2012*(2012 über 1) + ...
+ 1006*(2012 über 1006)
Während die obere Zeile offenbar durch 2012 teilbar ist, bleibt die untere zu untersuchen. Dabei reicht es festzustellen, ob (2012 über 1006) gerade ist. Das kann man per Induktion oder Rechnerei machen - aber es geht auch anders: (2012 über 1006) ist die Zahl der Möglichkeiten, 1006 Elemente aus 2012 auszuwählen. Nun gibt es aber zu jeder solcher Möglichkeit auch die Möglichkeit, genau die anderen 1006 Elemente auszuwählen. Also muss (2012 über 1006) durch 2 teilbar sein. Und damit ist 1006*(2012 über 1006) durch 2012 teilbar.
Zusammenfassung: Die Summe wird in drei Teile aufgeteilt. Zwei Summanden sind durch 2012 teilbar, der dritte ergibt bei der Division durch 2012 den Rest 16.
Die Antwort ist demnach 16.
Freirunde, habe gerade kein schönes Rätsel.
@Rest:
Zerlege die Summe zunächst in
(2012 über 0) + (2012 über 1) + ... + (2012 über 2012)
+ 0*(2012 über 0) + 1*... + 2012*(2012 über 2012)
Der erste Teil gibt genau 2^2012, was äquivalent zu 16 (mod 2012) ist. Kann man nachrechnen, auch wenn es auf dem Papier etwas Aufwand bedeutet.
Da (2012 über k) = (2012 über 2012-k), kann man die Summanden des zweiten Teils jeweils von außen paarweise zusammenfassen zu
2012*(2012 über 0) + 2012*(2012 über 1) + ...
+ 1006*(2012 über 1006)
Während die obere Zeile offenbar durch 2012 teilbar ist, bleibt die untere zu untersuchen. Dabei reicht es festzustellen, ob (2012 über 1006) gerade ist. Das kann man per Induktion oder Rechnerei machen - aber es geht auch anders: (2012 über 1006) ist die Zahl der Möglichkeiten, 1006 Elemente aus 2012 auszuwählen. Nun gibt es aber zu jeder solcher Möglichkeit auch die Möglichkeit, genau die anderen 1006 Elemente auszuwählen. Also muss (2012 über 1006) durch 2 teilbar sein. Und damit ist 1006*(2012 über 1006) durch 2012 teilbar.
Zusammenfassung: Die Summe wird in drei Teile aufgeteilt. Zwei Summanden sind durch 2012 teilbar, der dritte ergibt bei der Division durch 2012 den Rest 16.
Die Antwort ist demnach 16.
Freirunde, habe gerade kein schönes Rätsel.
Zuletzt bearbeitet:
- Mitglied seit
- 22.03.2008
- Beiträge
- 1.672
- Reaktionen
- 0
Eben mal wieder eine schöne Aufgabe in einem Buch gefunden:
(copyright Alan Beardon, Algebra and Geometry)
Zu zeigen ist also Abgeschlossenheit und Assoziativität der Verknüpfung, sowie Existenz eines neutralen Elements und eines inversen Elements zu jedem Element.
Wem es zu dumm ist, der soll es halt einfach nicht machen![::]:](/forum/data/assets/smilies/pleased.gif "::]: ::]:")
(copyright Alan Beardon, Algebra and Geometry)
Zu zeigen ist also Abgeschlossenheit und Assoziativität der Verknüpfung, sowie Existenz eines neutralen Elements und eines inversen Elements zu jedem Element.
Wem es zu dumm ist, der soll es halt einfach nicht machen
- Mitglied seit
- 23.11.2004
- Beiträge
- 1.142
- Reaktionen
- 8
1. es kann nicht -1 herauskommen:
-1 = x+y+xy => (x+1)(y+1)=0
Dies hat nur eine Lösung, wenn entweder x oder y -1 sind, welche nicht in G liegen. Daher ist das erste Gruppenaxiom trivialerweise erfüllt.
2. Das neutrale Element ist 0.
3. Assoziativität: (x*y)*z = (x+y+xy)*z = x+y+z+xy+xz+yz+xyz=x*(y*z)
4. Das inverse Element von x ist -x/(1+x)
Der Rest dürfte trivial sein.
Neues Rätsel: Beweisen Sie, dass es keien Menge gibt, deren Mächtigkeit zwischen der der natürlichen und der der reellen Zahlen liegt.
-1 = x+y+xy => (x+1)(y+1)=0
Dies hat nur eine Lösung, wenn entweder x oder y -1 sind, welche nicht in G liegen. Daher ist das erste Gruppenaxiom trivialerweise erfüllt.
2. Das neutrale Element ist 0.
3. Assoziativität: (x*y)*z = (x+y+xy)*z = x+y+z+xy+xz+yz+xyz=x*(y*z)
4. Das inverse Element von x ist -x/(1+x)
Der Rest dürfte trivial sein.
Neues Rätsel: Beweisen Sie, dass es keien Menge gibt, deren Mächtigkeit zwischen der der natürlichen und der der reellen Zahlen liegt.
- Mitglied seit
- 22.03.2008
- Beiträge
- 1.672
- Reaktionen
- 0
Neues Rätsel: Beweisen Sie, dass es keien Menge gibt, deren Mächtigkeit zwischen der der natürlichen und der der reellen Zahlen liegt.
- Mitglied seit
- 22.03.2008
- Beiträge
- 1.672
- Reaktionen
- 0
Da die Kontinuumshypothese erwiesenermaßen weder im Widerspruch zu Zermelo-Fraenkel steht, noch bewiesen werden kann, können wir sie einfach als Axiom annehmen. Oder noch besser, das Gegenteil:
Axiom9001: Es gibt eine Menge S, die mächtiger ist als N, aber weniger mächtig als R.
So, hier hast du deine Menge, Rätsel gelöst
Axiom9001: Es gibt eine Menge S, die mächtiger ist als N, aber weniger mächtig als R.
So, hier hast du deine Menge, Rätsel gelöst
Gelöschtes Mitglied 160054
Guest
Könnte man das, dann stünde das ja im Widerspruch zu Kurt Gödels Satz, dass die Kontinuumshypothese nicht im Widerspruch zum Rest der Mathematik steht, kokoreio bakareio
aber das weißt du eh alles, also stop trolling
Dann frage ich mich aber, wie es sein kann, dass sie existiert, aber nicht angegeben werden kann oO
Gelöschtes Mitglied 160054
Guest
Gerade gelesen: anscheinend schon
vllt findet irgendwann ja doch wer nen Fehler in den Beweisen
- Mitglied seit
- 22.03.2008
- Beiträge
- 1.672
- Reaktionen
- 0
jo könnte ich mir bei solchen Dingen auch immer ganz gut vorstellen ^^
hab die beweise ja auch selbst nicht angeschaut. Oder vielleicht werden irgendwann auch bessere Grundlagen für die Mathematik gefunden als die Mengenlehre, und es eröffnen sich ganz andere Möglichkeiten und Unmöglichkeiten.
hab die beweise ja auch selbst nicht angeschaut. Oder vielleicht werden irgendwann auch bessere Grundlagen für die Mathematik gefunden als die Mengenlehre, und es eröffnen sich ganz andere Möglichkeiten und Unmöglichkeiten.
Gelöschtes Mitglied 160054
Guest
dann kann man auch gleich mal die quantenphysik umbasteln, so dass sie ähhhhhh weniger seltsam wirkt
- Mitglied seit
- 22.03.2008
- Beiträge
- 1.672
- Reaktionen
- 0
und die Evolutionstheorie sodass sie sich mit der Bibel vereinbaren lässt 
edit:
.. womit ich aber nicht sagen will, dass ich ein Anzweifeln der Quantenmechanik für ähnlich lächerlich halte wie die Evolutionstheorie aufgrund der Bibel anzuzweifeln. (nunja von einem anderen Standpunkt ist ja selbst das ganz vernünftig, aber vielleicht nicht von einem wissenschaftlichen Sichtpunkt.)
Ich hab irgendwann vor einigen Jahren beschlossen, dass ich nicht an Physik glaube : )
Inzwischen ist mir die Physik wieder ein bisschen sympathischer, aber ganz überezeugt bin ich nicht. Und dass die Theorien, die wir heute haben, optimal sind, glaubt in der Physik, glaube ich, eh fast niemand.
edit:
.. womit ich aber nicht sagen will, dass ich ein Anzweifeln der Quantenmechanik für ähnlich lächerlich halte wie die Evolutionstheorie aufgrund der Bibel anzuzweifeln. (nunja von einem anderen Standpunkt ist ja selbst das ganz vernünftig, aber vielleicht nicht von einem wissenschaftlichen Sichtpunkt.)
Ich hab irgendwann vor einigen Jahren beschlossen, dass ich nicht an Physik glaube : )
Inzwischen ist mir die Physik wieder ein bisschen sympathischer, aber ganz überezeugt bin ich nicht. Und dass die Theorien, die wir heute haben, optimal sind, glaubt in der Physik, glaube ich, eh fast niemand.
Zuletzt bearbeitet:
Gelöschtes Mitglied 160054
Guest
und die Evolutionstheorie sodass sie sich mit der Bibel vereinbaren lässt
bibel und fehler will ja leider niemand hören
Aber nochmal zurück zu der nicht angebbaren(lol "bb"?) menge:
sie hat dann als eigenschaft das sie nicht angebbar ist, irgendwie ist mein gehirn dann verunsichert ob das nicht identisch mit "nicht existent" ist.
- Mitglied seit
- 22.03.2008
- Beiträge
- 1.672
- Reaktionen
- 0
hmjo das geht jetzt schon ziemlich ins philosophische hier.
Es gibt ja auch den konstruktivistischen ANsatz, dass man quasi sagt, was nicht konstruiert werden kann, das exisitert auch nicht, oder so.
http://de.wikipedia.org/wiki/Konstruktivistische_Mathematik
Ist eigentlich nüchtern betrachtet fast vernünftiger als die Mathematik, wie sie heute betrieben wird, aber macht vermutlich auch nicht so viel Spaß : D
Es gibt ja auch den konstruktivistischen ANsatz, dass man quasi sagt, was nicht konstruiert werden kann, das exisitert auch nicht, oder so.
http://de.wikipedia.org/wiki/Konstruktivistische_Mathematik
Ist eigentlich nüchtern betrachtet fast vernünftiger als die Mathematik, wie sie heute betrieben wird, aber macht vermutlich auch nicht so viel Spaß : D
Gelöschtes Mitglied 160054
Guest
Find sowelche beweise teilweise auch geiler um ehrlich zu sein^^
Aber mir gehts eher um das "wenn man es tatsächlich schaffte das zu konstruieren, wäre es falsch". Das ist irgendwie hmm wie sage ich es am besten: "UARGH"
- Mitglied seit
- 22.03.2008
- Beiträge
- 1.672
- Reaktionen
- 0
Man weiß einfach nicht ob es solche Mengen gibt, und kann es durch logisches Schlussfolgern aus den Axiomen der Mengenlehre nicht feststellen.
Es gibt ja auch Mengen, deren Mächtigkeit man nicht weiß, und es gibt bestimmt auch Mengen, deren Mächtigkeit garnicht feststellbar ist. Unter denen könnte ja so eine sein, deren Mächtigkeit eigentlich zwischen der von N und der von R liegt.
Man kann jedenfalls nicht, wenn man von einer Menge nur weiß, dass ihre Mächtigkeit größer als die von N ist und kleiner-gleich der von R, darauf schließen, dass sie gleich der Mächtigkeit von R sein muss, weil es könnte immer theoretisch noch etwas dazwischen sein.
edit:
d.h. es wäre denkbar, dass man durchaus auf so eine Menge stößt, jedoch nicht feststellen kann, dass ihre Mächtigkeit größer als die von N und kleiner als die von R ist.
Es gibt ja auch Mengen, deren Mächtigkeit man nicht weiß, und es gibt bestimmt auch Mengen, deren Mächtigkeit garnicht feststellbar ist. Unter denen könnte ja so eine sein, deren Mächtigkeit eigentlich zwischen der von N und der von R liegt.
Man kann jedenfalls nicht, wenn man von einer Menge nur weiß, dass ihre Mächtigkeit größer als die von N ist und kleiner-gleich der von R, darauf schließen, dass sie gleich der Mächtigkeit von R sein muss, weil es könnte immer theoretisch noch etwas dazwischen sein.
edit:
d.h. es wäre denkbar, dass man durchaus auf so eine Menge stößt, jedoch nicht feststellen kann, dass ihre Mächtigkeit größer als die von N und kleiner als die von R ist.
Zuletzt bearbeitet:
Du unterliegst ihren Gesetzen dennoch, und es ist diesen egal was du davon hälst
.Und die Konzepte der Quantenmechanik sind sehr gut experimentell abgesichert. Lediglich bei der Interpretation herrscht ein gewisser Spielraum, aber "shut up and calculate" klappt trotzdem.
"existiert, ist aber nicht konstruierbar" ist noch schlimmer im Rahmen des Auswahlaxioms, das so lustige Späße wie Kugelvervielfältigung durch Verschieben von 6 Teilen davon zulässt.
- Mitglied seit
- 22.03.2008
- Beiträge
- 1.672
- Reaktionen
- 0
Hier mal wieder etwas zum knobeln:
rätsel#29:
Man bestimme alle Funktionen, die auf der Menge der nicht negativen reellen Zahlen definiert sind, nur nicht negative reelle Werte annehmen und die folgenden drei Bedingungen erfüllen:
a) f(x*f(y)) * f(y) = f(x+y) für alle nichtnegativen reellen Zahlen x,y
b) f(2) = 0
c) f(x) != 0 , 0<=x<2 (also wenn x€[0,2), dann ist f(x) ungleich 0 )
rätsel#29:
Man bestimme alle Funktionen, die auf der Menge der nicht negativen reellen Zahlen definiert sind, nur nicht negative reelle Werte annehmen und die folgenden drei Bedingungen erfüllen:
a) f(x*f(y)) * f(y) = f(x+y) für alle nichtnegativen reellen Zahlen x,y
b) f(2) = 0
c) f(x) != 0 , 0<=x<2 (also wenn x€[0,2), dann ist f(x) ungleich 0 )
Setze y=2 in die Gleichung ein und nutze f(2)=0:
f(x*0) * 0 = f(x+2)
=> f(x+2)=0 für alle x>=0, also f(x)=0 für alle x>=2
Setze x=y=0 ein:
f(0) * f(0) = f(0)
Da f(0)!=0, gilt f(0)=1
Setze nun y=x-2 ein und betrachte 0<=x,y<2:
f(x*f(x-2)) * f(x-2) = f(2)
f(x*f(x-2)) * f(x-2) = 0
f(x-2)!=0 aufgrund von Bedingung c, also muss f(x*f(x-2))=0 sein und (wegen Bedingung c und meiner obigen Betrachtung) also x*f(x-2)>2 für alle 0<=x<2.
Für 0<x<2 lässt sich das umformen zu f(x)>2/(2-x)
Hmm... da lässt sich sicher noch mehr herausfinden, aber ich muss jetzt erstmal weg.
f(x*0) * 0 = f(x+2)
=> f(x+2)=0 für alle x>=0, also f(x)=0 für alle x>=2
Setze x=y=0 ein:
f(0) * f(0) = f(0)
Da f(0)!=0, gilt f(0)=1
Setze nun y=x-2 ein und betrachte 0<=x,y<2:
f(x*f(x-2)) * f(x-2) = f(2)
f(x*f(x-2)) * f(x-2) = 0
f(x-2)!=0 aufgrund von Bedingung c, also muss f(x*f(x-2))=0 sein und (wegen Bedingung c und meiner obigen Betrachtung) also x*f(x-2)>2 für alle 0<=x<2.
Für 0<x<2 lässt sich das umformen zu f(x)>2/(2-x)
Hmm... da lässt sich sicher noch mehr herausfinden, aber ich muss jetzt erstmal weg.
Zuletzt bearbeitet:
- Mitglied seit
- 28.07.2006
- Beiträge
- 12
- Reaktionen
- 0
Behauptung: die Lösung ist f(x)=2/(2-x) für x<2, sonst 0
Beweis:
für x>=2 hats mfb bereits bewiesen, der Rest bezieht sich immer auf x<2.
mfb hat auch gezeigt, dass f(x)>= 2/(2-x) (>=, da aus f(x*f(x-2))=0, x*f(x-2)>=2 folgt, da f(x)=0 für x>=2)
bleibt also f(x)<= 2/(2-x) zu zeigen:
Beweis durch Widerspruch: Angenommen es gibt eine Lösung f(x) mit f(x) > 2/(2-x) d.h. f(x)=2/(2-x)+e(x) mit e(x)>0.
Wähle dann d(x)=e(x)*(2-x)/(e(x)+2/(2-x)).
Da e(x)>0 und x<2 ist d überall defniniert und d(x)>0.
Setze y<2 und x=2-y-d(y), dann gilt: (mit d:=d(y) und e:=e(y))
x*f(y) = x*2/(2-y)+x*e = 2-2*d/(2-y)+(2-y-d)e
= 2-2*e/(e+2/(2-y))+(2-y)*e-e^2*(2-y)/(e+2/(2-y))
= 2+1/(e+2/(2-y))*[-2*e+(2-y)e*(e+2/(2-y))-e^2*(2-y)]
= 2+1/(e+2/(2-y))*0
= 2
und somit
f(x*f(y))*f(y)=f(2)*f(y)=0 nach b)
aber f(x+y) = f(2-d(y)) != 0 nach c) da d(y)>0 -> Widerspruch.
Also muss die Annahme falsch sein, und somit f(x)<= 2/(2-x).
q.e.d.
es ist viel zu spät, ich werde versuchen morgen ein Rätsel zu finden, wenn jemand eins auf Lager hat, kann er es auch gerne stellen.
Beweis:
für x>=2 hats mfb bereits bewiesen, der Rest bezieht sich immer auf x<2.
mfb hat auch gezeigt, dass f(x)>= 2/(2-x) (>=, da aus f(x*f(x-2))=0, x*f(x-2)>=2 folgt, da f(x)=0 für x>=2)
bleibt also f(x)<= 2/(2-x) zu zeigen:
Beweis durch Widerspruch: Angenommen es gibt eine Lösung f(x) mit f(x) > 2/(2-x) d.h. f(x)=2/(2-x)+e(x) mit e(x)>0.
Wähle dann d(x)=e(x)*(2-x)/(e(x)+2/(2-x)).
Da e(x)>0 und x<2 ist d überall defniniert und d(x)>0.
Setze y<2 und x=2-y-d(y), dann gilt: (mit d:=d(y) und e:=e(y))
x*f(y) = x*2/(2-y)+x*e = 2-2*d/(2-y)+(2-y-d)e
= 2-2*e/(e+2/(2-y))+(2-y)*e-e^2*(2-y)/(e+2/(2-y))
= 2+1/(e+2/(2-y))*[-2*e+(2-y)e*(e+2/(2-y))-e^2*(2-y)]
= 2+1/(e+2/(2-y))*0
= 2
und somit
f(x*f(y))*f(y)=f(2)*f(y)=0 nach b)
aber f(x+y) = f(2-d(y)) != 0 nach c) da d(y)>0 -> Widerspruch.
Also muss die Annahme falsch sein, und somit f(x)<= 2/(2-x).
q.e.d.
es ist viel zu spät, ich werde versuchen morgen ein Rätsel zu finden, wenn jemand eins auf Lager hat, kann er es auch gerne stellen.
- Mitglied seit
- 22.03.2008
- Beiträge
- 1.672
- Reaktionen
- 0
Jo, sehr gut, in team work gelöst sozusagen 
Zu zeigen wäre natürlich noch, dass die Funktion f, die durch f(x)=2/(2-x) für 0<=x<2 und f(x)=0 für x>=2 definiert ist, tatsächlich eine Lösung der Funktionalgleichung ist.
Denn es wurde ja nur gezeigt, dass wenn eine Funktion f die FUnktionalgleichung erfüllt, sie so aussehen muss, nicht aber umgekehrt, dass wenn eine FUnktion so aussieht, sie auch die Funktionalgl. erfüllt. Das lässt sich aber relativ schnell überprüfen (mit bisschen Fallunterscheidungen bzgl x und y), und es ist jedenfalls wirklich eine Lösung. ^^
Der zweite Teil des Beweises ist ja ziemlich kompliziert geworden mit dem e(x) und dem d(x) ^^. Man kann's auch einfacher beweisen:
Angenommen es gibt ein 0<x<2 mit f(x)>2/(2-x). Dann ist auch 2-x > 2/f(x). Setze in der Funktionalgleichung 2/f(x) für x ein, und x für y, und erhalte einen Widerspruch.
f( 2/f(x) * f(x) ) * f(x) = f( 2/f(x) + x )
Zu zeigen wäre natürlich noch, dass die Funktion f, die durch f(x)=2/(2-x) für 0<=x<2 und f(x)=0 für x>=2 definiert ist, tatsächlich eine Lösung der Funktionalgleichung ist.
Denn es wurde ja nur gezeigt, dass wenn eine Funktion f die FUnktionalgleichung erfüllt, sie so aussehen muss, nicht aber umgekehrt, dass wenn eine FUnktion so aussieht, sie auch die Funktionalgl. erfüllt. Das lässt sich aber relativ schnell überprüfen (mit bisschen Fallunterscheidungen bzgl x und y), und es ist jedenfalls wirklich eine Lösung. ^^
Der zweite Teil des Beweises ist ja ziemlich kompliziert geworden mit dem e(x) und dem d(x) ^^. Man kann's auch einfacher beweisen:
Angenommen es gibt ein 0<x<2 mit f(x)>2/(2-x). Dann ist auch 2-x > 2/f(x). Setze in der Funktionalgleichung 2/f(x) für x ein, und x für y, und erhalte einen Widerspruch.
f( 2/f(x) * f(x) ) * f(x) = f( 2/f(x) + x )
Zuletzt bearbeitet:
- Mitglied seit
- 27.07.2010
- Beiträge
- 3.605
- Reaktionen
- 0
Beh: Für alle ganzen Zahlen n gilt
42 | n^7− n
Bew: 42 = 2 * 3* 7. Wir zeigen also n^7-n = 0 mod 2,3,7.
n^7 - n = n (n^6-1) = n * (1+n+n^2+n^3+n^4+n^5) (n-1)
Offensichtlich ist entweder n oder n-1 = 0 mod 2.
Ist n oder n-1 = 0 mod 3, so ist n^7 -n = 0 mod 3. Bleibt also der Fall n = 2 mod 3. Einsetzen liefert: (1+n^2+n^3+n^4+n^5) = 0 mod 3.
nach dem kleinen Fermat (n^6-1) = 0 mod 7.
Also ist der gesamte Ausdruck mod 42 gleich Null.
42 | n^7− n
Bew: 42 = 2 * 3* 7. Wir zeigen also n^7-n = 0 mod 2,3,7.
n^7 - n = n (n^6-1) = n * (1+n+n^2+n^3+n^4+n^5) (n-1)
Offensichtlich ist entweder n oder n-1 = 0 mod 2.
Ist n oder n-1 = 0 mod 3, so ist n^7 -n = 0 mod 3. Bleibt also der Fall n = 2 mod 3. Einsetzen liefert: (1+n^2+n^3+n^4+n^5) = 0 mod 3.
nach dem kleinen Fermat (n^6-1) = 0 mod 7.
Also ist der gesamte Ausdruck mod 42 gleich Null.
Zuletzt bearbeitet:
Rätsel 31:
Klassiker:
Zeige, dass es gleich viele [natürliche Zahlen] und [gerade natürliche Zahlen] gibt.
Klassiker:
Zeige, dass es gleich viele [natürliche Zahlen] und [gerade natürliche Zahlen] gibt.
- Mitglied seit
- 22.03.2008
- Beiträge
- 1.672
- Reaktionen
- 0
Hmm ist irgendwie ungut als "Rätsel" weil entweder kennt man den Begriff der Mächtigkeit, dann weiß man die Lösung vermutlich eh schon, oder man kennt den Begriff nicht, dann wird man die Aussage aber auch schwer "zeigen" können, weil man ja nicht weiß wie die entsprechenden Begriffe definiert sind, also man wird sich nicht sicher sein, was genau "gleich viele" bedeutet.
d.h. die Hauptschwierigkeit ist einfach, die Angabe zu verstehen.
Also Lösung:
Sei N die Menge der natürlichen Zahlen, 2N die Menge der geraden natürlichen Zahlen.
Sei f:N -> 2N
für alle n€N: f(n) = 2n
Dann ist f injektiv:
f(m)=f(n)
=> 2m=2n
=> m=n
und f ist surjektiv:
Sei m € 2N beliebig. Dann gibt es ein k€N sodass m=2k (sonst wäre m ja nicht eine gerade Zahl), und somit f(k)=m.
Also f bijektiv und die Mengen sind somit gleichmächtig.
rätsel#32
Seien x,y,z reelle Zahlen mit x²+y²+z²=1.
Beweise, dass
12x + 3y + 4z <= 13
d.h. die Hauptschwierigkeit ist einfach, die Angabe zu verstehen.
Also Lösung:
Sei N die Menge der natürlichen Zahlen, 2N die Menge der geraden natürlichen Zahlen.
Sei f:N -> 2N
für alle n€N: f(n) = 2n
Dann ist f injektiv:
f(m)=f(n)
=> 2m=2n
=> m=n
und f ist surjektiv:
Sei m € 2N beliebig. Dann gibt es ein k€N sodass m=2k (sonst wäre m ja nicht eine gerade Zahl), und somit f(k)=m.
Also f bijektiv und die Mengen sind somit gleichmächtig.
rätsel#32
Seien x,y,z reelle Zahlen mit x²+y²+z²=1.
Beweise, dass
12x + 3y + 4z <= 13
Och, Pärchen (n,2n) machen klappt doch ziemlich intuitiv auch.
Zu deinem Rätsel fällt mir außer dem langweiligen Standardweg gerade keine schöne Herleitung ein.
Dass man mit quadratischer Addition schnell aufs Maximum kommt weiß ich auch unabhängig davon, aber irgendein Ein- oder Zweizeiler dazu sehe ich gerade nicht.
Zu deinem Rätsel fällt mir außer dem langweiligen Standardweg gerade keine schöne Herleitung ein.
Dass man mit quadratischer Addition schnell aufs Maximum kommt weiß ich auch unabhängig davon, aber irgendein Ein- oder Zweizeiler dazu sehe ich gerade nicht.
- Mitglied seit
- 22.03.2008
- Beiträge
- 1.672
- Reaktionen
- 0
Ich glaube nicht dass man hier mit quadratischer Ergänzung direkt ans Ziel kommt. Probiers aus!
Wieso Ergänzung? Addition.
sqrt(12^2+3^2+4^2)=13
Analog erhält man auch den Vektor (x,y,z) als 1/13*(12,3,4). Dass dieser, eingesetzt in deine Funktion, direkt 13 ergibt, sollte klar sein.
Man kann das ganze Zeug als Funktion f(x,y)=12x + 3y + 4z(x,y) betrachten, ableiten etc. und erhält diese Lösung auch. Aber wenn man keinen schönen Beweis dafür braucht (oder es einmal allgemein hergeleitet hat), kann man die Lösung auch direkt hinschreiben.
Geht auch in n!=3 Dimensionen analog.
sqrt(12^2+3^2+4^2)=13
Analog erhält man auch den Vektor (x,y,z) als 1/13*(12,3,4). Dass dieser, eingesetzt in deine Funktion, direkt 13 ergibt, sollte klar sein.
Man kann das ganze Zeug als Funktion f(x,y)=12x + 3y + 4z(x,y) betrachten, ableiten etc. und erhält diese Lösung auch. Aber wenn man keinen schönen Beweis dafür braucht (oder es einmal allgemein hergeleitet hat), kann man die Lösung auch direkt hinschreiben.
Geht auch in n!=3 Dimensionen analog.
- Mitglied seit
- 22.03.2008
- Beiträge
- 1.672
- Reaktionen
- 0
Ich verstehe deine Methode nicht 8[
Aber sie basiert vermutlich auch auf der Cauchy-Schwarz Ungleichung, aus der ich die Ungleichung gefolgert hätte. (siehe dazu hier http://starcraft2.ingame.de/forum/showthread.php?t=217167)
Man kann auch dem in dem thread diskutierten Beweis folgen um direkt einen elementaren Beweis für die Ungl. zu erhalten:
12x + 3y + 4z <= 13
(multipliziere die Ungl. mit 2/13 und erhalte: )
24/13 x + 6/13 y + 8/13 z <= 2 = (x² + y² + z²) + (12/13)² + (3/13)² + (4/13)²
(und jetzt kann man alles auf die rechte Seite bringen und zu Quadraten zusammenfassen.)
0 <= (x - 12/13)² + (y - 3/13)² + (z - 4/13)²
und die Ungl. ist wahr weil Quadrate immer größergleich 0 sind.
Aber wie gesagt, wenn man die Cauchy Schwarz Ungleichung kennt, dann muss man nur einsetzen und fertig : )
jo, ich habe jetzt aufgelöst weil die Ungl. für mfb anscheinend sowieso offensichtlich war.
Wer will, kann das nächste Rätsel posten ^^
Aber sie basiert vermutlich auch auf der Cauchy-Schwarz Ungleichung, aus der ich die Ungleichung gefolgert hätte. (siehe dazu hier http://starcraft2.ingame.de/forum/showthread.php?t=217167)
Man kann auch dem in dem thread diskutierten Beweis folgen um direkt einen elementaren Beweis für die Ungl. zu erhalten:
12x + 3y + 4z <= 13
(multipliziere die Ungl. mit 2/13 und erhalte: )
24/13 x + 6/13 y + 8/13 z <= 2 = (x² + y² + z²) + (12/13)² + (3/13)² + (4/13)²
(und jetzt kann man alles auf die rechte Seite bringen und zu Quadraten zusammenfassen.)
0 <= (x - 12/13)² + (y - 3/13)² + (z - 4/13)²
und die Ungl. ist wahr weil Quadrate immer größergleich 0 sind.
Aber wie gesagt, wenn man die Cauchy Schwarz Ungleichung kennt, dann muss man nur einsetzen und fertig : )
jo, ich habe jetzt aufgelöst weil die Ungl. für mfb anscheinend sowieso offensichtlich war.
Wer will, kann das nächste Rätsel posten ^^
Zuletzt bearbeitet:
