Mathe Rätsel Marathon

[Brusko651]

So, nachdem hier mal wieder zu wenig los ist für meinen Geschmack...

ich poste ein Mathe Rätsel. Wer es löst, kann das nächste Rätsel posten, und so weiter. You get the idea.

Vom Schwierigkeitsgrad her sollten sie eher so sein, dass man sie mit Schulwissen lösen kann (sind ja nicht alle Dipl. Ingenieur hier im Forum), darf aber auch mal schwerer (oder leichter ^^) sein, Ausnahmen bestätigen die Regel.

Ok, here we go:

Rätsel#1
Sei ABC ein gleichseitiges Dreieck.
P sei ein zufällig ausgewählter Punkt in dem Dreieck.
Wie groß ist die Wahrscheinlichkeit, dass der Winkel APB größer als 120° ist?
(APB ist der Winkel, der durch die beiden Strahlen PA und PB eingeschlossen wird)

 

[Brusko651]

hmm, nachdem ich vorher extra gesagt habe, dass die Rätsel mit Schul Wissen lösbar sein sollen, wäre es vielleicht etwas unfair, wenn ich gleich bei diesem ersten Rätsel nicht noch einen kleinen Tipp dazu geben würde:

Tipp:
Nachdem den wahrscheinlich doch die meisten nicht aus der Schule kennen, weise ich auf den Zentrum-Peripherie-Winkel-Satz, bzw Kreiswinkel Satz hin, der beim Lösen des Rätsels hilfreich, oder vielleicht sogar notwendig, ist.
http://de.wikipedia.org/wiki/Kreiswinkel

kurz:
alle Winkel an einen Kreis, die von der selben Kreissehne ausgehen sind gleich groß (Peripheriewinkel), und zwar halb so groß wie der entsprechende Zentriwinkel, zur Kreismitte.
(illustriert durch den blauen, grünen und roten Winkel in dem Bild hier )

 

[ferdi1337]

so um die 33% ?

 

[Brusko651]

nope, ist noch ein bisschen mehr als 1/3.
war aber auch meine erste Vermutung, als ich das Rätsel zum ersten mal angeschaut habe (hab es auch nicht selbst erfunden).

 

[sesslor]

Stimmt 0.4728?

 

[zoiX]

Wenn ja, dann erbitte ich hiermit den Rechenweg ^^

 

[Brusko651]

Jap, das stimmt!
Aber bitte wirklich deinen Lösungsweg posten ^^
Und dann poste ein neues Rätsel ^^

edit:
also die exakte lösung ist eigentlich

aber sesslors Lösung lass ich natürlich gelten

 

[sesslor]

Genau, das hatte ich auch. Der Loesungsweg ist relativ lang, aber straight-forward. Man nimmt den Kreis, der durch die Punkte A, B und den Mittelpunkt des Dreiecks geht, und berechnet dessen Schnittflaeche mit dem Dreieck. Dann noch durch die Gesamtflaeche des Dreiecks teilen, und fertig.

 

[sesslor]

Ok, ich machs mir einfach für das nächste Rätsel: Beweist Batman's Kreiswinkelsatz (siehe 2. Post im Thread).

 

[Myta]

das klingt irgendwie weniger nach einem rätsel als nach einer relativ einfachen, wenn auch evtl etwas langwierigeren rechenaufgabe.

in polarkoordinaten rechnen müsste das ganze vereinfachen wenn man den mittelpunkt des kreises auf den ursprung legt.

 

[Benrath]

fand die idee eigentlich gut, nicht dass ich jetzt lust hätte die Aufagben zu lösen. ABer hätte auch gedacht das sich der TE eher knobelige Rätzel vorgestellt hätte, die man mal eben auf nem kleinen Zettel lösen kann. ABer dann war scheinbar schon die ursprungsaufgabe nicht ganz korrekt.

 

[mfb]

Die erste Aufgabe ließ sich doch gut auf einem kleinen Zettel lösen .

Bzgl. sesslors Aufgabe:
Hmm... mal einen neuen Ansatz ausprobieren. Imba Painstskills incoming.
Alle Kreise haben Radius 1.

Zunächst wird gezeigt, dass der Winkel beta (ß) die Hälfte der Kreisbogenlänge (linker Teil) ist:
alpha+2*gamma = pi => gamma=pi/2-alpha/2 (Innenwinkelsumme im Dreieck)
gamma+beta=pi/2 => beta=alpha/2
alpha ist aber genau gleich der Länge des Kreisbogens => fertig.
Für alpha>pi sieht die Skizze etwas deformiert aus, die Gleichungen behalten aber ihre Gültigkeit.

Nun betrachte folgende Skizze:

Für zwei beliebige Kreissehnen, die sich an einem Punkt des Kreises schneiden, betrachte die Winkel alpha und beta zwischen ihnen und der Kreistangente - was dem Beta von oben entspricht. Nun ist der Abschnitt 1 des Kreisbogens genau 2*beta, und die Summe aus 1+2 ist 2*alpha. Der Abschnitt 2 hat also die Länge 2*(alpha-beta) und damit ist seine Länge nur vom Öffnungswinkel gamma=alpha-beta zwischen den beiden Sehnen abhängig.
Und damit bin ich bereits fertig - vom Mittelpunkt des Kreises aus hat der Abschnitt genau seine Kreisbogenlänge als Winkel, und vom Rand aus eben die Hälfte.


Neues Rätsel:

Der böser Herrscher hat in seiner Burg einen Kerker mit 100 Zellen und je einem Gefangenen darin. Eines Tages lässt er von einem Boten alle Zellentüren öffnen, denn er will den Gefangenen die Freiheit schenken. Die Wachen sorgen dafür, dass kein Gefangener vor 0:00 Uhr seine Zelle verlässt. Im Laufe des Abends vergisst der Herrscher seine Barmherzigkeit und schickt einen zweiten Boten, der den Zustand jeder zweiten Zelle (beginnend mit der zweiten) ändert: Ist sie offen, schließt er sie ab, ist sie abgeschlossen, schließt er sie auf. Danach schickt er einen dritten Boten, der den Zustand jeder dritten Zelle (beginnend mit der dritten) ändert, ... , dann den n-ten Boten, der jede n. Zelle ändert und so weiter. Kurz vor 0:00 Uhr Uhr dreht der 100. Bote den Schlüssel in nur einer Tür - der 100. - herum und alle Gefangenen, deren Zellentüren offen sind, dürfen gehen.
Welche Gefangenen sind es?


Zusatzfrage: Nimm an, dass der n. Bote nicht mit der n. Zelle beginnt, sondern seine erste Zelle gleichverteilt unter den ersten n auswählt. Der 3. Bote könnte beispielsweise bei 2 beginnen, dann besucht er 2,5,8,...
Welche Wahrscheinlichkeit für die Freilassung ergibt sich für die verschiedenen Zellen?

 

[ze_german]

ausgangsrätsel:

Alle Zellen deren Nummern eine gerade Anzahl an Teilern haben bleiben geschlossen.

 

[Brusko651]

hmm, nachdem ich jetzt auch schon seit einer Stunde an meinem Beweis für den Batman Winkel Satz getippt habe, poste ich ihn auch noch
Als neues Rätsel gilt natürlich das aus mfbs post.

kurz zu meiner Notation,
Ich schreibe W(ABC) für den Winkel ABC. (den Winkel bei B)

so, erstmal formuliere ich den Satz exakt aus, damit klar ist, was ich eigentlich beweisen möchte:
Satz: (Zentrum-Peripherie-Winkel-Satz) Seien A,B zwei Punkte auf einem Kreis k mit dem Mittelpunk M, sodass M nicht zwischen A und B liegt (d.h., sie liegen nicht auf einer Linie).
Dann unterteilen die Punkte A,B den Kreis in 2 Kreisbögen, einen großen Bogen b_1, in dessen Innerem (bzw eigentlich im entsprechenden Kreissegment) der Mittelpunkt M liegt und einen kleinen Bogen, b_2, in dem der Punkt M nicht liegt.
Sei P ein Punkt auf dem großen Bogen b_1. Dann ist W(APB)=W(AMB)/2.
weiters:
Ist Q ein Punkt auf dem kleinen Bogen b_2, dann ist W(AQB) = 180° - W(APB).
weiters: (Satz von Thales)
Wenn die Punkte A,B hingegen so liegen, dass M auf einer Geraden mit ihnen liegt, also dass AB der Durchmesser des Kreises ist, dann ist W(AMB)=180° und für jeden Punkt P auf dem Kreis mit P != A und P!= B gilt W(APB)=90°.
(Der Satz von Thales ist ein Spezialfall des Kreiswinkelsatzes, ich werde ihn aber extra beweisen.)

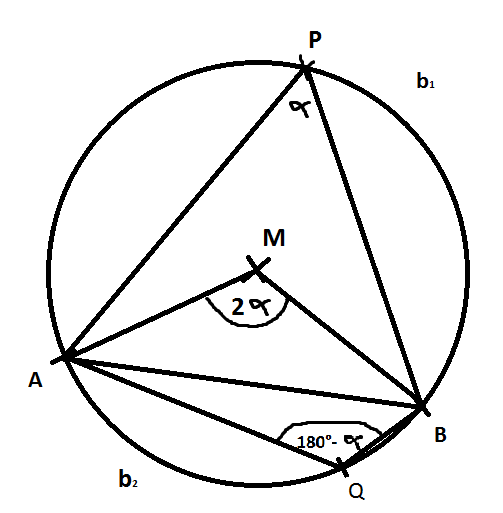
Hier ein Bild dazu:

Beweis:
Seien also zunächst A,B nicht auf einer Linie mit M, und P sei auf dem Bogen b_1.
Dann sind 3 Fälle zu unterscheiden:
Fall1: M liegt im Inneren des Dreiecks ABP.
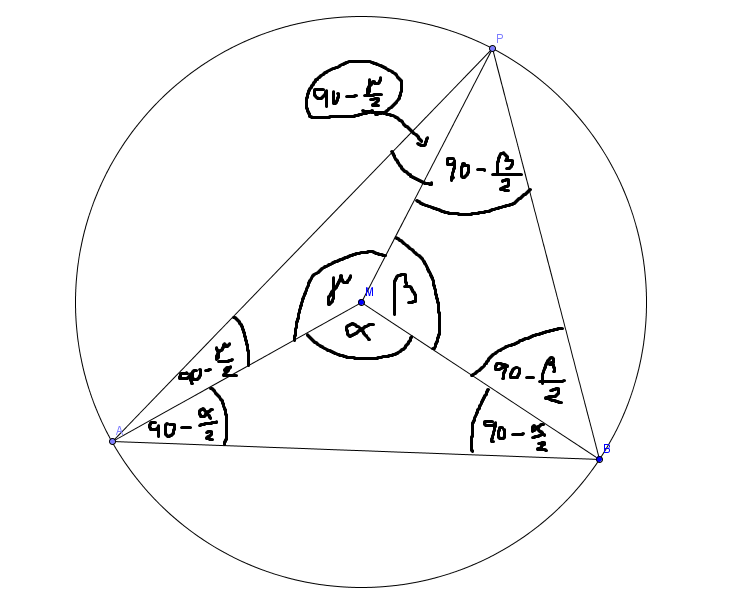
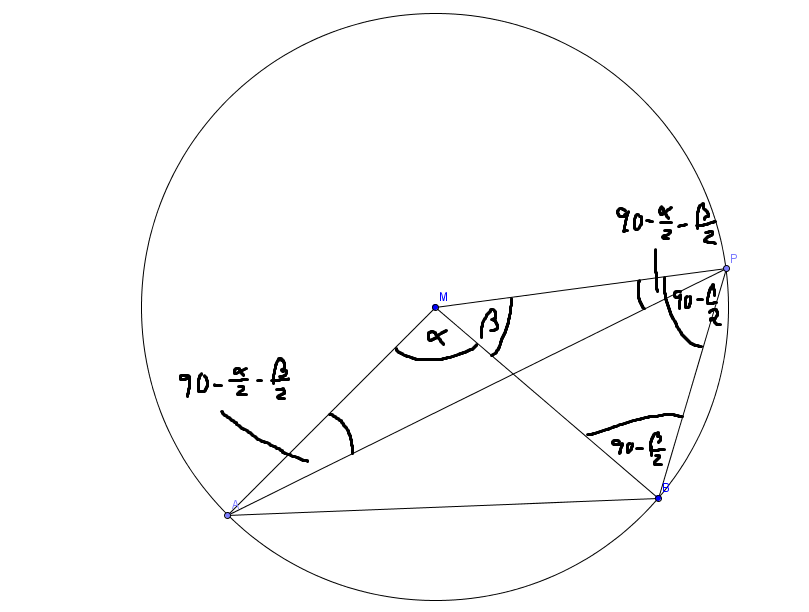
Dann bezeichne ich W(AMB) mit Alpha und W(BMP)=Beta und W(AMP)=Gamma.

Da die Dreiecke ABM, APM und BMP jeweils gleichschenklig sind, kann man daraus (Winkelsumme im Dreieck = 180°) auf die Winkel am Rand schließen (siehe das Bild oben.).
Insbesondere ist W(APB) = 180 - Gamma/2 - Beta/2.

Man sieht aber: Alpha + Beta + Gamma = 360°.
Also 180° = Alpha/2 + Beta/2 + Gamma/2.
Und somit ist W(APB) = Alpha/2 + Beta/2 + Gamma/2 - Gamma/2 - Beta/2 = Alpha/2
und der erste Fall ist somit erledigt.

Fall2: Der Mittelpunkt M liegt außerhalb des Dreiecks APB.
Ich gehe davon aus, dass der Punkt P "rechts" von M liegt, wie in der Zeichnung unten. Der andere Fall müsste analog gehen.
Ich bezeichneW(AMB) = Alpha, W(BMP) = Beta.

Da das Dreieck BMP gleichschenkling ist, können wir schließen, dass W(BPM)=W(MBP)=90-Beta/2 ist.

Ebenso ist das Dreieck MAP gleichschenklig und W(MPA)= W(MAP) = 90 - Alpha/2 - Beta/2.

Also ist der Winkel W(APB) = W(BPM) - W(MPA) = 90 - Beta/2 - (90 - Alpha/2 - Beta/2) = Alpha/2
und somit ist auch dieser Fall abgeschlossen.

Fall3: Der Punkt M liegt auf der Seite AP oder auf der Seite BP.
o.B.d.A. legen wir einfach fest, dass er auf der Seite AP liegt. (der andere Fall geht analog).

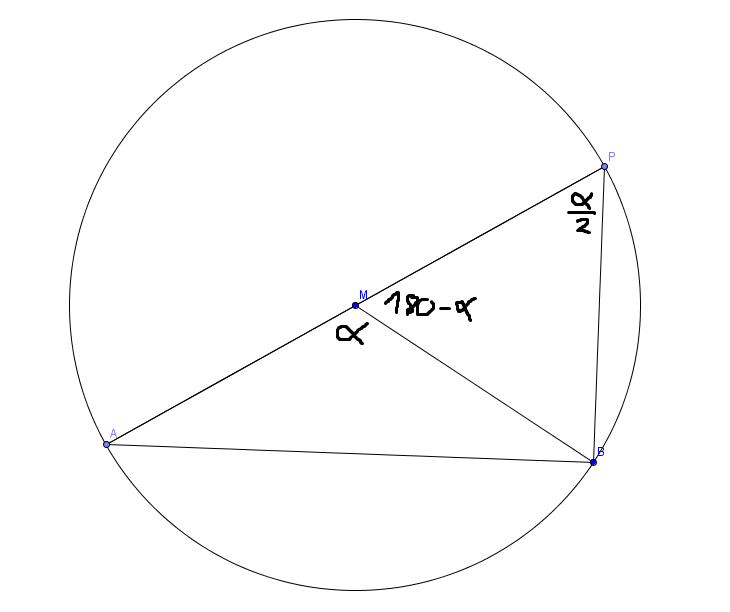
Sei W(AMB)=Alpha. Dann ist W(BMP) = 180-Alpha und aus der Gleichschenkligkeit des Dreiecks BMP kann man sehen dass W(BMP)=Alpha/2 sein muss, damit die WInkelsumme im Dreieck 180° ergibt.


Somit ist tatsächlich in jedem Fall W(APB) = W(AMP)/2.

Nun zum zweiten Teil des Satzes:
Sei Q ein Punkt auf dem gegenüberliegenden Bogen b_2.
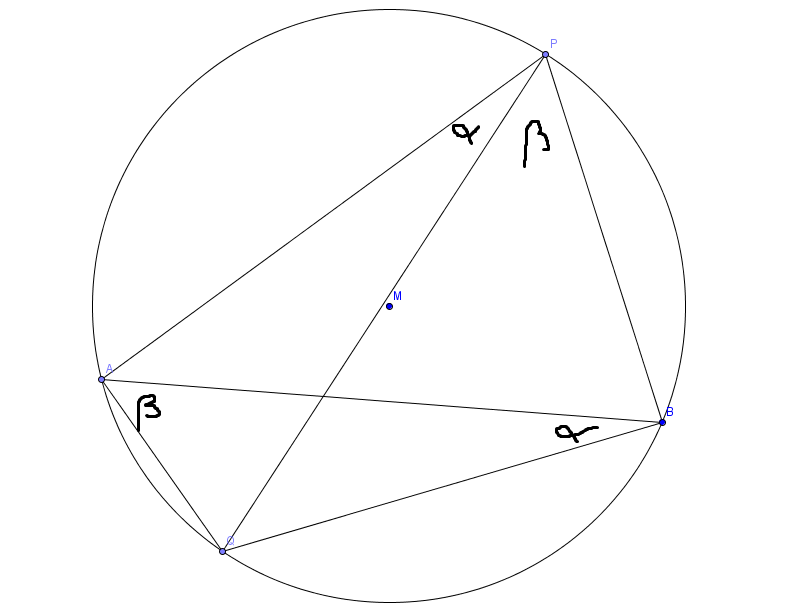
Aus dem soeben bewiesenen, können wir sehen, dass W(APQ) = W(ABQ).
(Beides sind Peripheriewinkel über der Sehne AQ (und der Mittelpunkt M liegt auf der richtigen Seite der Sehne). Wir bezeichnen W(APQ) = W(ABQ) = Alpha

Ebenso W(QAB) = W(QPB) = Beta.
Aus der Winkelsumme des Dreiecks ABQ kann man nun sehen, dass W(AQB) = 180 - Alpha - Beta = 180 - W(APB)
und auch dieser Teil des Satzes ist somit bewiesen.

Zuletzt wird noch der Fall behandelt, in dem der Punkt M zwischen A und B liegt, also wo AB den Durchmesser des Kreises bilden. (Satz von Thales)

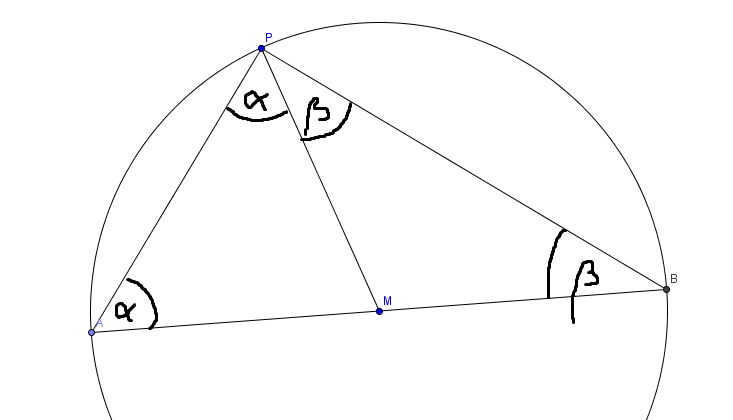
Ich bezeichne W(APM) = Alpha und W(BPM) = Beta. Dann ist wegen gleichschenkliger Dreiecke auch W(MAP) = Alpha und W(MBP) = Beta.
Die Winkelsumme im Dreieck ist 180° also 180° = 2Alpha + 2Beta.
=> 90° = Alpha + Beta = W(APB).
q.e.d.

 

[Brusko651]

Zusatzfrage: Nimm an, dass der n. Bote nicht mit der n. Zelle beginnt, sondern seine erste Zelle gleichverteilt unter den ersten n auswählt. Der 3. Bote könnte beispielsweise bei 2 beginnen, dann besucht er 2,5,8,...
Welche Wahrscheinlichkeit für die Freilassung ergibt sich für die verschiedenen Zellen?

ersteinmal ist leicht zu sehen:
Die Wahrscheinlichkeit ist für jede Tür gleich. Denn egal wo die Tür ist, die Wahrscheinlichkeit ist erstmal 1, dass sie geöffnet wird, dann, im nächsten Schritt, 1/2 dass sie wieder geschlossen wird, dann im nächsten Schritt wiederum 1/3, dass ihr Zustand geändert wird. Und allgemein ist für den n-ten Boten die Wahrscheinlichkeit 1/n dass er den Zustand unserer Tür ändern wird (unabhängig davon welche Tür es ist, die wir betrachten.)

Nun kann man durch vollständige Induktion zeigen, dass die Wahrscheinlichkeit für die Tür, am Ende offen zu sein, 1/2 ist.
Induktionsanfang: nach dem zweiten Boten ist die Wahrscheinlichkeit 1/2 dass sie offen ist, und 1/2 dass sie geschlossen ist.

Wir gehen nun davon aus, dass nach dem Durchgang des k-ten Boten (1<k<100) die Wahrscheinlichkeit 1/2 ist, dass die Tür offen ist, und zeigen, dass die Wahrscheinlichkeit dann auch nach dem Durchgang des k+1 - ten Boten 1/2 ist.
Das ist am folgenden Wahrscheinlichkeitsbaum ersichtlich:

Wahrscheinlichkeit dass sie nach dem k+1 ten Boten offen ist ist also
1/2 * k/(k+1) + 1/2 * 1/(k+1) = 1/2
und ebenso ist die Wahrscheinlichkeit dass sie geschlossen ist 1/2.

Somit ist auch nach dem 100ten Boten die Wahrscheinlichkeit, dass die Tür offen ist, 1/2.

Folgt daraus eigentlich dass am Ende genau die Hälfte der Türen offen ist? Ich bin mir nicht sicher, ich glaube aber nicht ^^
(edit: ne folgt natürlich nicht, habs ausprobiert, wie es ist, wenn man nur 4 Türen hätte, und hat sich natürlich als Unsinn herausgestellt. Der Erwartungswert für die Anzahl an offenen Türen müsste aber 50 sein, denke ich. Aber auch da bin ich mir nicht sicher.)

ze_german hat das eigentliche Rätsel gelöst also kann er auch das nächste Rätsel stellen

 

[ze_german]

Ich hab spontan nichts geplant; Wer also was am Start hat, darf sich gern dazu bemüssigt fühlen eins zu stellen

 

[Brusko651]

rätsel #4:
Löse das Gleichungssystem:

(wobei x,y reelle Zahlen sind.)

 

[Myta]

x=1, y=-1
(hab keine zeit ein neues zu stellen, darf jemand anders machen)

 

[zoiX]

Muss nicht als neues Rätsel verstanden werden, interessiert mich aber: Wie groß ist bei der Gefangenensache mit zufällig gewählter Starttür die Wahrscheinlichkeit, dass am Ende ALLE Türen geschlossen / offen sind?

 

[mfb]

Alle Zellen deren Nummern eine gerade Anzahl an Teilern haben bleiben geschlossen.

Es gibt eine viel kürzere Beschreibung für diese Zahlen, aber ist ok.

@Bruce Wayne:
PS: Im Komplexen hat dein System mehrere Lösungen


@zoiX: Ich fürchte, das wird eine schlimme Rechnerei für jedes n. Die Korrelation zwischen zwei Zellen habe ich mal ausgerechnet, die ist schon nicht mehr trivial. Meine Vermutung: Mehr als 1/2^n

 

[Brusko651]

Es gibt eine viel kürzere Beschreibung für diese Zahlen, aber ist ok.

alle Zahlen, die keine Quadratzahlen sind. : )

(kann man sich leicht aus http://de.wikipedia.org/wiki/Teileranzahlfunktion überlegen, dass nur Quadratzahlen eine ungerade Teileranzahl haben)

hmm, das bedeutet eigentlich, dass tatsächlich alle bis auf 10 arme Kerle freigelassen werden lol.
edit: achso ne umgekehrt, nur 10 Leute werden freigelassen.

 

[emp]

Weil wir die letzten zwei Stunden im TS drüber diskutiert haben.

 

[Brusko651]

find ich gut ^_^
also diese eine Linie ist anscheinend eine Tangente, also müsste der Winkel MTP (der eh nicht gesucht ist, aber..) 90° sein.
Somit ist der Winkel PMT dann 90-25°, also 65°.
Gamma ist dementsprechend 180-65=115°.

Das Dreieck AMT ist gleichschenklig, also muss Alpha die Hälfte von 180-115 sein, also Alpha= 32,5°.

Und Beta ist nach dem Zentrum-Peripherie Winkel Satz die Hälfte von Gamma also 57,5°.


Hab gerade kein neues Rätsel auf Lager, ich poste im Laufe des Tages noch eines.
€: Ich editier das neue Rätsel dann hier dazu, will nicht so viele doppelposts machen.

edit:

Rätsel#7:
(naja ich sag einfach mal es ist #7^^.)
Wir ziehen drei Karten von einem normalen 52-Karten Deck (4 Farben, 13 Werte), was ist die Wahrscheinlichkeit, dass die erste Karte nicht Pik ist, die zweite Karte eine Zehn ist, und die dritte Karte keine Figur (König, Dame, Bube) ist.

 

[ipskab]

würde ich dieses rätsel irgendwo lesen, wärs mir sofort klar, was ich zu tun hätte, aber wenn es jetzt ein "rätsel" ist, frage ich mich was die schwierigkeit darin ist.

in meinem jugendlichen leichtsinn würde ich es einfach "auszählen".
13 karten sind Pik, also bleiben 52-13 = 39 übrig.
es gibt viermal die 10, also 4.
4*3=12 figuren, also 52-12 = 40 Karten
alle möglichkeiten sind bei 3x ziehen: 52*51*50 (ohne zurücklegen)
P = (39*4*40)/(52*51*50) = 4,7%

und warum ist das nun falsch? (bin rechter noob auf dem gebiet^^)

 

[Brusko651]

Nachdem du eine 10 bereits weggenommen hast, sind nur mehr 39 Karten übrig, die keine Figuren sind. d.h. richtig wäre
FALSCH
(39*4*39)/(52*51*50)
bzw
3/4 * 1/13 * 39/52
=3/68
/FALSCH
aber war ja ungefähr richtig; poste bitte ein neues Rätsel, falls dir eines einfällt ^^

edit: argghh, ich hab kompletten Unsinn erzählt.
korrekt ist:
3/4 * 1/13 * 39/51
bzw das ist
(39 * 4 * 39) / (52 * 52 * 51)

und das ist dann 3/68 ^^

 

[ipskab]

"Einer Mathematiker zu seinen zwei Freunden: Ich lasse euch zwei Zahlen raten-einem sage ich derer Produkt und dem zweiten dann ihre Summe. Es handelt sich um volle Zahlen, jede ist größer als 1 und ihre Summe ist kleiner als 99. Er flüstert einem das Produkt der beiden Zahlen und dem anderen die Summe der Zahlen.
Der Erste, der das Produkt kennt sagt: "Das weiß ich nicht"
Der Zweite, der die Summe kennt sagt: "Das habe ich gewußt, das du es nicht wissen wirst"
Der Erste, der das Produkt kennt ruft:" Ja? Dann weiß is es".
Der Zweite, der die Summe kennt sagt: "Dann weiß ich es auch"
Die Frage: Um welche Zahlen handelt es sich?"

 

[sesslor]

Nachdem du eine 10 bereits weggenommen hast, sind nur mehr 39 Karten übrig, die keine Figuren sind. d.h. richtig wäre
FALSCH
(39*4*39)/(52*51*50)
bzw
3/4 * 1/13 * 39/52
=3/68
/FALSCH
aber war ja ungefähr richtig; poste bitte ein neues Rätsel, falls dir eines einfällt ^^

edit: argghh, ich hab kompletten Unsinn erzählt.
korrekt ist:
3/4 * 1/13 * 39/51
bzw das ist
(39 * 4 * 39) / (52 * 52 * 51)

und das ist dann 3/68 ^^

Fallunterscheidung nicht vergessen. Wenn du schon beim ersten Mal eine Zehn ziehst, sinkt die Wahrscheinlichkeit, beim zweiten Mal eine zu ziehen. Das selbe gilt fuer die Figur.

 

[Brusko651]

Fallunterscheidung nicht vergessen. Wenn du schon beim ersten Mal eine Zehn ziehst, sinkt die Wahrscheinlichkeit, beim zweiten Mal eine zu ziehen. Das selbe gilt fuer die Figur.

jap genau, das war im Grunde genommen der Fehler, den ikskap gemacht hat.

Man kann sich aber in dem Fall sparen, eine Fallunterscheidung zur ersten gezogenen Karte zu machen, weil wenn man nur schaut ob sie Pik ist, dann könnte sie ja genau so gut eine zehn, wie ein König , oder sonst irgendetwas sein, und es ändert sich nichts an der Wahrscheinlichkeit, dass die nächste Karte eine 10 ist (1/13).
Auf gewisse Weise sind Farbe/Wert der Karten unabhängig voneinander, und das kann man hier ausnutzen.

Das wird noch deutlicher wenn man die Reihenfolge ändert, in der die Karten gezogen werden.
Ich tu also die erste Karte um 2 Karten nach hinten und frag mich dann, wie groß die Wahrscheinlichkeit, ist dass ich zuerst eine 10 ziehe, dann eine nicht-Figuren Karte, und dann eine nicht-pik Karte.
Dann ist natürlich erstmal die Wahrscheinlichkeit 1/13, dass die vorderste Karte eine 10 ist, und, wenn das der Fall ist, noch 39/51, dass die zweite Karte nicht König/Dame/Bub ist. So, und wenn man jetzt die letzte Karte anschaut, dann ist natürlich noch immer die Wahrscheinlichkeit 1/4, dass sie Pik ist, einfach, weil 1/4 der Karten in dem Deck Pik sind ^^

Wenn man eine ausführliche Fallunterscheidung macht, dann kommt man auch auf das selbe Ergebnis (3/68), ist aber recht umständlich.

 

[sesslor]

Ipskab: die Zahlen sind 4 und 13, falls ich keinen Fehler gemacht habe. Ich werd mir mal ein Raetsel ueberlegen.

 

[Maiev]

Bist du ernsthaft alleine darauf gekommen in der kurzen zeit, ohne, dass du das rätsel kanntest?
Ich kanns mir kaum vorstellen, wenn doch, respekt.

 

[Brusko651]

hmm "kurze Zeit", waren doch eh 2-3 Stunden, seit das Rätsel gepostet wurde.

 

[sesslor]

Ich bin selbst draufgekommen, aber mit matlab-Unterstuetzung. Mit Zettel und Stift haette ich das so schnell sicher nicht geschafft.

 

[sesslor]

Ich werd jetzt mal ein neues Raetsel stellen, diesmal ist es wirklich eher ein Raetsel und keine Rechenaufgabe:

In einem Kloster leben 1000 Moenche, 100 haben blaue Augen und der Rest schwarze Augen. Es gibt keine Spiegel und die Moenche kommunizieren nicht miteinander ueber ihre Augenfarbe, es gibt also fuer keinen Moench die Moeglichkeit, seine eigene Augenfarbe auf direktem Wege herauszufinden. Die Moenche wissen auch nicht, wieviele von ihnen insgesamt schwarze bzw. blaue Augen haben. Einmal am Tag treffen sich die Moenche, um zusammen zu speisen. Dabei hat sieht jeder Moench die Augenfarben aller andern Moenche. Es gilt die Regel, dass ein Moench in der Nacht Selbstmord begehen muss, sobald er sicher weiss, dass seine Augenfarbe blau ist.

Die Moenche leben also viele Jahre so vor sich hin, ohne dass sich irgendeiner von ihnen umbringt. Doch eines Tages kommt ein Fremder ins Kloster und sagt beim gemeinsamen Speisen, so dass es alle Moenche hoeren koennen: "Ich habe einen Moench mit blauen Augen gesehen." Dann verlaesst er das Kloster wieder. In der 100. Nacht, die auf dieses Ereignis folgt, bringen sich alle Moenche mit blauen Augen selbst um.

Die Aufgabe ist nun, zu erklaeren, warum dies passieren konnte.

 

[Brusko651]

hatten wir halt auch schonmal im Rätsel thread im CPZ. oder im Mathe/Physik? es gab glaub ich 2-3 Rätsel threads in den letzten paar Jahren und dieses Rätsel kommt fast immer zur Sprache ^^
deswegen bin ich auch mit dem thread ein bisschen mehr Richtung mathe gegangen, weil die ganzen standard Rätsel hatten wir schon in den anderen threads.
Aber die, die's noch nicht kennen (oder sich nicht mehr erinnern können ), können ja mal dran rum rätseln

 

[Myta]

im letzten rätsel thread kam das sogar zweimal innerhalb von zwei seiten vor.
du hast aber eine wichtige angabe vergessen: alle Mönche sind perfekte Logiker, wenn etwas logisch geschlussfolgert werden kann dann tun sie dies augenblicklich. und jeder mönch weiß über diese tatsache bescheid.

 

[sesslor]

Ok, war mir nicht klar, dass das Raetsel schon so oft da war. Dann kann irgendwer anders ja ein neues posten.

@Myta: dass Moenche in allen Belangen perfekte Nazi-Uebermenschen sind, sollte doch Basisraetselwissen sein.

 

[Brusko651]

Ok ich verweise zur Lösung dann einfach mal auf http://starcraft2.ingame.de/forum/showthread.php?t=205661, Seite 1 ab Post 24.

Und dann poste ich wieder ein neues Rätsel.
Ist leider schon wieder Wahrscheinlichkeitsrechnung, dafür muss ich mich entschuldigen, hab halt viele gute von der Sorte auf Lager

rätsel #10
Aus dem Intervall [0,10] werden zwei reelle Zahlen x und y zufällig ausgewählt.
Wie groß ist die Wahrscheinlichkeit, dass 5x + 9y < 45 ?

 

[Gelöschtes Mitglied 160054]

Die Wahrscheinlichkeit das x und y gezogen werden ist gleich Null.

 

[Brusko651]

nene x und y SIND die Zahlen, die durch einen Zufallsprozess gezogen wurden ^^
Die Frage ist, wie wahrscheinlich ist, dass die Ungleichung 5x + 9y < 45 erfüllt ist.

 

[Gelöschtes Mitglied 160054]

Wie so häufig bei statistischen Fragen schwimme ich ein wenig:

Für eine reelle Zahl x ist die Wahrscheinlichkeit das sie gezogen wird identisch Null. Davon unabhängig:
Wenn man die Ungleichung umformt erhält man

x < 9-9/5 y

Also kann man erstmal abschätzen das y element von [0,5) ist und x in (0,9) liegt, wobei die konkrete Einschränkung abhängig ist von y.
Die Wahrscheinlichkeit das eine Ziehung im Bereich [0,5) liegt ist 50%.
Jetzt ist die Frage, wie die Ziehung zugeordnet wird? Ziehe ich ein Paar und kann dann beliebig verteilen?