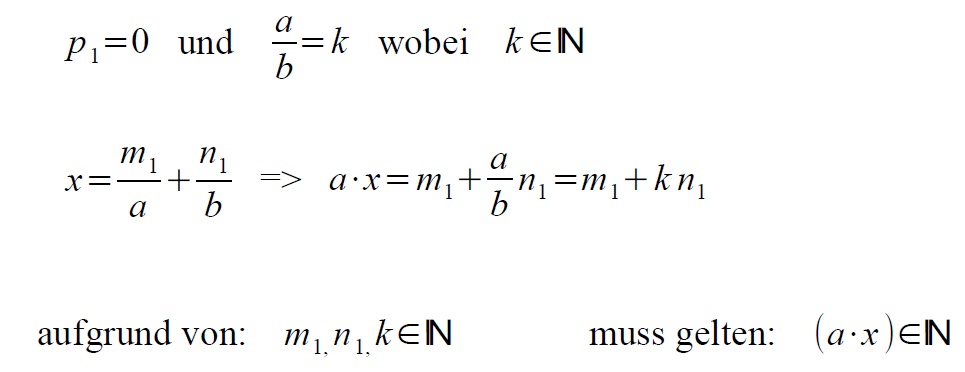hey,
ich hab glaube ich gerade ein ziemliches Brett vor dem Kopf.
Ich habe folgende Formel:
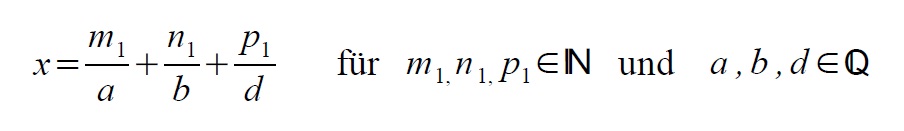
Hierbei sind a,b,d konstante (positive) Raummaße und m,n,p variable, natürliche Zahlen.
Mein Problem:
Ich muss zeigen, dass es, für irgendein konstantes x, mehr Kombinationsmöglichkeiten m,n,p gibt, wenn die Raummaße ganzzahlige Vielfache voneinander sind.
Eine einfache Annahme:

für dieses x gibt es mehr Lösungen für m,n als wenn a und b nicht ganzzahlige Vielfache von einander sind:

Ich weiß, ist alles nicht wirklich korrekt ausgedrückt, aber ich hoffe ich konnte das Problem verständlich erklären?
Ist eigentlich ja schon logisch vorstellbar, aber wie kann ich das mathematisch offensichtlich darlegen?
ich hab glaube ich gerade ein ziemliches Brett vor dem Kopf.
Ich habe folgende Formel:
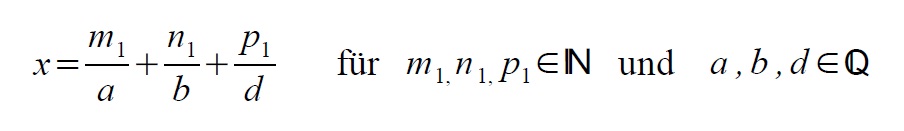
Hierbei sind a,b,d konstante (positive) Raummaße und m,n,p variable, natürliche Zahlen.
Mein Problem:
Ich muss zeigen, dass es, für irgendein konstantes x, mehr Kombinationsmöglichkeiten m,n,p gibt, wenn die Raummaße ganzzahlige Vielfache voneinander sind.
Eine einfache Annahme:

für dieses x gibt es mehr Lösungen für m,n als wenn a und b nicht ganzzahlige Vielfache von einander sind:

Ich weiß, ist alles nicht wirklich korrekt ausgedrückt, aber ich hoffe ich konnte das Problem verständlich erklären?
Ist eigentlich ja schon logisch vorstellbar, aber wie kann ich das mathematisch offensichtlich darlegen?
Zuletzt bearbeitet: