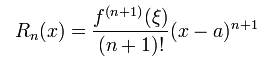Unter welchen Bedingungen konvergiert die Taylorreihe einer Funktion gegen eben diese

[Gelöschtes Mitglied 160054]

Dafür habe ich keine Regeln gefunden muss ich gestehen. Gibt nur immer den Hinweis, dass die Taylorreihe nicht gegen die Funktion konvergieren muss.
Nur um das klarzustellen: "gegen die Funktion konvergieren" meine ich im Sinne: Taylorreihe konvergiert und sie innerhalb des Konvergenzradiuses (wert-)identisch mit der entwickelten Funktion.

 

[sesslor]

Naja, wenn die Funktion im gesamten Konvergenzbereich analytisch ist, konvergiert auch die Taylorreihe darin zu dem Funktionswert. Es kann nur irgendwas passieren, wenn die Funktion nicht analytisch ist, soweit ich weiss.

 

[Gelöschtes Mitglied 160054]

Naja, wenn die Funktion im gesamten Konvergenzbereich analytisch ist, konvergiert auch die Taylorreihe darin zu dem Funktionswert. Es kann nur irgendwas passieren, wenn die Funktion nicht analytisch ist, soweit ich weiss.

Naja, wenn sie analytisch ist, dann lässt sich sich als potenzreihe darstellen und eben diese ist ja (zumindest lokal, um wikipedia zu zitieren) die taylorreihendarstellung der funktion. zumindest auf den ersten blick beisst sich da was selbst in den schwanz

 

[sesslor]

Hier stand Unsinn, hatte die Definition von analytisch falsch im Kopf.

Edit: Eventuell koennte dir die komplexe Analysis weiterhelfen. Anders als im reellen (was ich vorher faelschlicherwiese behauptet hatte), ist hier Analytizitaet und Differenzierbarkeit equivalent. Es reicht sogar, dass die Funktion einmal differenzierbar ist, dann ist sie automatisch unendlich oft differenzierbar und laesst sich als Potenzreihe schreiben.

Selbst wenn du im rellen bist, koennte dir eine Fortsetzung ins komplexe vielleicht weiterhelfen. Um was fuer eine Funktion geht es eigentlich, oder ist deine Frage allgemein?

 

[Gelöschtes Mitglied 160054]

Hier stand Unsinn, hatte die Definition von analytisch falsch im Kopf.

Edit: Eventuell koennte dir die komplexe Analysis weiterhelfen. Anders als im reellen (was ich vorher faelschlicherwiese behauptet hatte), ist hier Analytizitaet und Differenzierbarkeit equivalent. Es reicht sogar, dass die Funktion einmal differenzierbar ist, dann ist sie automatisch unendlich oft differenzierbar und laesst sich als Potenzreihe schreiben.

Selbst wenn du im rellen bist, koennte dir eine Fortsetzung ins komplexe vielleicht weiterhelfen. Um was fuer eine Funktion geht es eigentlich, oder ist deine Frage allgemein?

Ist eine allgemeine Frage.^^

 

[mfb]

Um zu prüfen, ob die Taylorreihe gegen die Funktion konvergiert, brauchst du eben Aussagen über die Funktion im ganzen relevanten Bereich.

Das übliche Beispiel ist hier f:R->R, f(x)=e^(-1/x^2) für x!=0, f(0)=0 im Reellen. Bei x=0 sind alle Ableitungen 0, die Taylorreihe hier ist also einfach g(x)=0 und hat damit einen Konvergenzradius von unendlich. Sie ist aber nur bei x=0 mit der Funktion identisch.

Im Komplexen reicht wie bereits erwähnt, dass die Funktion im relevanten Bereich einmal differenzierbar ist.

 

[Brusko651]

Ich beziehe mich jetzt nur auf reelle Funktionen, wie das bei komplexen ist, weiß ich nicht so genau.

Aber für reelle:

Man kann immer f darstellen durch
f(x) = p_n(x) + R_n(x)
("Taylorformel")

wobei p_n das Taylorpolynom ist, das aus den ersten n+1 Summanden der Taylorreihe mit Entwicklungspunkt x0 besteht (also die Summanden mit x^0 bis x^n), und R_n(x) das "Restglied", das eben genau den Wert annimmt, um welchen p_n daneben liegt.

Wenn nun für ein x€R das Restglied R_n(x) für n->unendlich gegen 0 konvergiert, dann bedeutet das, dass p_n(x) für n->unendlich gegen f(x) konvergiert.
Und genau dann konvergiert die Taylorreihe gegen die Funktion f (zumindest im Punkt x ^^)

Das ganze wären jetzt nur nutzlose Trivialitäten, wenn man nicht zum Glück für das Restglied R_n(x) explizite Darstellungen kennen würde.
Zum Beispiel gibt es da die Restglied Darstellung von Lagrange, die man mit Hilfe des Mittelwertsatzes beweisen kann:

(hier heißt der Entwicklungspunkt der Reihe jetzt a, nicht x0, wie ich oben geschrieben habe. Das Xi ist dabei irgendeine gewisse (nicht näher bekannte) reelle Zahl zwischen a und x.)

Das reicht auch schon aus, um etwa zu sehen, dass die Sinusfunktion gleich ihrer Potenzreihe ist.
Wir wissen (wenn wir die Ableitungen von Sinus bereits kennen), dass die (n+1)-te Ableitung von f entweder Sinus, cosinus, -sinus oder -cosinus sein wird. Somit wird das f'(n+1) (xi) in der Formel betragsmäßig sicher kleiner-gleich 1 sein. Der Entwicklungspunkt a ist die 0, den können wir also auch weglassen.
Somit |R_n(x)| <= x^(n+1) / (n+1)!
Und da die rechte Seite für n-> unendlich gegen 0 konvergiert, tut es also auch R_n(x).
Ähnlich kann man sich etwa auch aus einfach Eigenschaften der Exponentialfunktion überlegen, dass sie gegen ihre Taylorreihe konvergieren wird.
(beide Beispiele sind nicht unbedingt sinnvoll, da exp und sin ja meistens bereits über ihre Potenzreihe definiert werden.)

Also nochmal zusammenfassend: Die Funktion ist in einem Punkt x gleich ihrer Taylorreihe, wenn das Restglied gegen 0 konvergiert. Es gibt auch andere Darstellungen für das Restglied, als die von Lagrange, zB mit Integralen. Siehe dazu hier http://de.wikipedia.org/wiki/Taylor-Formel.

edit:
achja, Voraussetzung ist natürlich auch, dass die Funktion unendlich mal differenzierbar ist, sonst macht die Taylorreihe ja garkeinen Sinn.
Und zwar muss sie das glaube ich nicht nur in einem einzelnen Punkt sein, sondern auf einem ganzen Intervall. In meinem Buch steht es für eine auf einem offenen Intervall unendl. oft differenzierbare Funktion. Weiß nicht wie das dann ist wenn man etwa eine Funktion hat, die auf einem abgeschlossenen Intervall definiert ist

 

[Brusko651]

del plz.

 

[Gelöschtes Mitglied 160054]

Das kann nicht hinreichend sein.(siehe obiges Beispiel mit e^1/-x²).
Dort konvergiert trivialerweise für den Entwicklungspunkt x0 für alle x aus R das Restglied gegen Null. Trotzdem ist die Entwicklung nur für den Punkt gültig. Obwohl das Restglied für alle anderen x ebenso konvergiert.

 

[Brusko651]

Hast du meinen langen Post über das Restglied gelesen?
Im Fall von e^(-1/x^2) bildet eben das Restglied R_n(x) keine Nullfolge sofern x!=0.

edit: hab jetzt meinen doppel post oben zu einem post zusammenge-edit-ed.

 

[Gelöschtes Mitglied 160054]

Hast du meinen langen Post über das Restglied gelesen?
Im Fall von e^(-1/x^2) bildet eben das Restglied R_n(x) keine Nullfolge sofern x!=0.

hast du die beispielfunktion oben gelesen? es ging um f(x) = exp(1/-x²) für x>0 und f(x) = 0 f+r x = 0.
ist unendlich oft differenzierbar mit allen Ableitungen gleich Null im Ursprung. Restglied ist daher immer Null.

 

[Brusko651]

hast du die beispielfunktion oben gelesen? es ging um f(x) = exp(1/-x²) für x>0 und f(x) = 0 f+r x = 0.
ist unendlich oft differenzierbar mit allen Ableitungen gleich Null im Ursprung. Restglied ist daher immer Null.

Nope, die Taylorpolynome p_n sind immer 0. (und somit auch die Taylorreihe)

Somit folgt mit der Taylorformel sofort:
f(x) = p_n(x) + R_n(x)
f(x) = R_n(x)

Also ist für x != 0
R_n(x) konstant gleich e^(-1/x^2) > 0.

Ich glaube noch immer dass du nur meinen zweiten post gelesen hast. hab oben nämlich einen gosu-doppelpost gemacht : D

edit:
mit der Restglied Darstellung von Lagrange, die ich oben gepostet habe, kann man übrigens nicht den exakten Wert des Restglieds ausrechnen, weil man ja das xi nicht weiß.

 

[Gelöschtes Mitglied 160054]

nee, habe ich schon gelesen, hatte das nur anders in erinnerung. HMM, häää, vermutlich gings da doch um das "nur weils in einem punkt konvergiert, gilts nicht für alle blabla".

 

[mfb]

Das Restglied verwendet die Ableitungen an Punkten xi != 0 (i.A., kann auch mal 0 sein). Und dort hat mein Beispiel von 0 verschiedene Ableitungen. Da dieses xi selbst von x abhängen kann, ist die Darstellung des Restglieds längst nicht so explizit, wie sie aussieht, aber zumindest kann man damit die Größe nach oben abschätzen.